Çeliklerin Haddelenmesinde Malzeme Modelleme

Çeliklerin şekillendirilmesinde kullanılan başlıca şekillendirme metodu plastik şekillendirmedir. Plastik şekillendirme prosesi işlemin sıcaklığına bağlı olarak sıcak ve soğuk şekillendirme olarak adlandırılmaktadır. Çeliklere uygulanan soğuk deformasyon ile çok iyi tolerans değerleri ve daha pürüzsüz yüzeyler elde edilmeye çalışılmaktadır. Soğuk deformasyonun sağladığı bu faydaların yanında dislokasyon yoğunluğunu arttırması , sünekliği azaltması gibi istenmeyen durumlara da yol açmaktadır. Soğuk deformasyon sırasındaki oluşan bu dislokasyon yığılmaları genellikle tavlama ile giderilirken tavlama mekanizması içinde yeniden kristalleşme önemli bir yer tutmaktadır.
Sıcak deformasyonda ise işlem parametreleri olan sıcaklık ve genleme hızı altında malzeme deforme edilir. Bu esnada sıcaklığın katkısıyla soğuk deformasyona göre çok daha büyük miktarlarda genleşme sağlanabilmektedir. 0,5 Tm sıcaklık değerinin üzerindeki plastik deformasyon işlemlerinde atomlar tırmanma mekanizması ile hareket edip dislokasyon yığılmalarını önlerken gene bu sıcaklık değeri yeniden kristalleşmenin malzeme bünyesinde oluştuğu sıcaklık değeridir .
Haddeleme çeliklerin plastik şekillendirilmesi için kullanılan başlıca metottur. Çeliklerin haddelenmesi iki şekilde yapılır :
1.1 Sıcak Haddeleme
Yeniden kristalleşme sıcaklığı olan 0,5 Tm nin üzerinde meydana gelen haddeleme işlemine denir . İlk sıcak işleme işlemi birçok çelik üretimi için blum milinde yapılır . Blum mili 60 cm den 137 ye cm kadar ikili reversible merdanedir. Blum haddesi ingot yapısını bozduğundan bu iş tekrarlanan ısıtmalarla dikkatli bir şekilde yapılır . Blum haddelenmesi için alaşımlı büyük ingotun yaklaşık 25 defa haddeden geçmesi gerekir .Kütük istenilen ebata gelene dek bitirme haddelerde haddelenir. Diğer bir haddeleme yöntemi ise üniversal haddelemedir . Bu yöntemde ise bir merdane iki yatay dört dikey merdane ile kenar haddesi yapabilecek şekilde monte edilmiştir. Üniversal haddesi makaslanmaya ihtiyaç duymayan düzgün kenarlı levhalar haddeler. Bu haddeleme metodu ile ingot yalnızca uzunluğuna uzatıldığı için zıt yönde haddelemeye gerek duyulmaz .
1.2 Soğuk Haddeleme
Malzemenin yeniden kristalleşme sıcaklığının altında meydana gelen haddelemeye denir . Soğuk haddeleme çeliklerde sıcak haddelenmiş mamullere nazaran daha iyi çap toleransı ve düzgün yüzeyli şerit imalatı için kullanılır . Soğuk haddeleme neticesi malzeme bünyesinde meydana gelen yüzey sertliği mukavemeti arttırmak için kullanılabilir .


Çelikte dayanım artışı sağlamanın yollarından birisi de küçük tane boyutu elde etmektir. Haddeleme işleminde bunu sağlayan mekanizma yeniden kristalleşmedir. Sıcak haddelemeye maruz kalmış bir yapı çeliğinde ortalama tane boyutu 20 µm civarındadır [3]. Sıcak haddelemeden sonraki kontrollü bir soğuma süreci ile ortalama tane boyutu 5 ile 10 µm arasına düşürebilir [3]. Toparlanma, statik, dinamik ve metadinamik yeniden kristalleşme imalat süreci içinde meydana gelen ve içyapıyı belirleyen mekanizmalardır. Ostenit alanında haddelemede yeniden kristalleşme mekanizması baskındır. Ostenit alanına ısıtılmış çelikte haddeleme sıcaklığına , deformasyon miktarına ve deformasyon hızına bağlı olarak işlem öncesi statik yeniden kristalleşme, işlem anında dinamik yeniden kristalleşme görülebilir. Haddeleme sonrası soğuma sonucu ostenit ferrite , perlite yada beynite dönüşür . Dönüşümün kinetiği ve oda sıcaklığındaki iç yapının faz düzeni dönüşüm öncesi ostenit iç yapısından ve soğuma koşullarından doğrudan etkilenir. Çeliklerin haddelenmesinde dislokasyon yoğunluğu da oldukça artar. Sıcak haddelemede toparlanma ve yeniden kristalleşme mekanizmaları devreye girerek dislokasyon yoğunluğunu azaltır.
Bir çelik malzeme için oda sıcaklığında ortaya çıkacak haddeleme içyapısı, fazların türleri, şekilleri ve boyutları açısından haddeleme koşullarına bağlı olarak çok farklı olabilir. Bu sebeple, hem haddeleme esnasında meydana gelen içyapı oluşumunun fiziğini daha iyi anlayabilmek ve hem de son iç yapıyı doğru modelleyerek kalite kontrolünü sağlayabilmek için matematik modeller oldukça önemlidir. Haddelemedeki iç yapıyı bilebilmek için yeniden kristalleşme olayını, her pasodan sonraki tane boyutunu tanımlayabilmek gerekir. Ayrıca, haddeleme sonrasında meydana gelen metadinamik yeniden kristalleşmeyi ve yüksek sıcaklıkta oluşan tane büyümesi olaylarını dikkate almak da haddelemede malzeme modellemenin konusudur. Haddeleme içyapısı birçok değişkene bağlı olmakla beraber bir modelleme denkleminde esas olarak sıcaklık, deformasyon miktarı ve hızı ile, pasolar arası geçen süre bulunmalıdır.

2 . HADDELEME SÜRECİNDE İÇYAPIDA ETKİLİ OLAN MEKANİZMALAR VE MODELLENMESİ

2.1. Toparlanma

Toparlanma ile içyapıdaki dislokasyon yoğunluğu önemli oranda değişmemekte, ancak dislokasyonlar yeniden düzenlenmektedir. Bu nedenle pekleşmenin sağladığı dayanım artışını kaybetmeden süneklik artabilmektedir. Yüksek sıcaklıklarda şekil vermede, plastik deformasyon esnasında dislokasyonlar oluşur oluşmaz toparlanma mekanizması aktif hale gelir. Toparlanma sonucu oluşan yeni dislokasyon dağılımı, plastik deformasyonla meydana gelen orman dislokasyonlarına göre enerji bakımından çok daha tercih edilebilir durumdadır. Toparlanmada malzeme yapısındaki dislokasyonlar daha düşük enerjiye sahip oldukları poliganizasyon adı verilen bir düzene girerler. Bu durumda dislokasyonlar gerçekte küçük açılı tane sınırı meydana getirmektedir (Lee Youngseog, 2004). Sıcaklık yeterince yüksekse, deformasyon sonrası statik toparlanma süresince dislokasyon dağılımı değişirken, dislokasyon yoğunluğu bir miktar azalabildiğinden malzeme bünyesinde yumuşama meydana gelir. Yapılan araştırmalarda elde edilen bilgilere göre toparlanma mekanizması ile meydana gelen maksimum yumuşama miktarı yaklaşık olarak 20 civarındadır ( Serajzadeh Siamak ,2006)

Deformasyon anında Tane boyutları aynı kalırken, dislokasyon yoğunluğu artar ve alt tane oluşumu gözlenir. Mekanizma kararlı hale geldiğinde ise dislokasyon yoğunluğu ve alt tane boyutları sabit hale gelir. Dinamik toparlanmada ise, dislokasyonların dağılımı haddeleme esnasında yeniden düzenlenir.

2.2 Yeniden Kristalleşme
Yeniden kristalleşme mekanizmasın ile şekil verme sonucu yoğun dislokasyona sahip olan tane yapısı, dislokasyon yoğunluğu az yeni yapıya dönüşür. Bu süreçte malzemenin mikroyapısında değişim meydana gelirken, kristal yapısı ve makroyapısında değişim gözlenmez. Yeni tanelerin çekirdeklenmesi ile birlikte dislokasyon yoğunluğu hızlı bir şekilde azalır. Yeniden kristalleşmeye bağlı olarak azalan dislokasyon yoğunluğu nedeniyle malzemenin pekleşme ile sağladığı dayanım artışı değerinde düşüş başlar (Lee Youngseog, 2004).Yeniden kristalleşmenin verdiği yeni tanelerin boyutu daha küçük olursa dayanımda artış gözlemlenir. Bilindiği gibi, Hall-Petch eşitliğine göre malzemede dayanım değeri azalan tane boyutuna bağlı olarak artış gösterir.
(2.1)

Hall – Petch eşitliği tane sınırlarının dislokasyon hareketini engelleyen sınırlar olduğu prensibi üzerine kurulmuştur. Yeniden kristalleşme haddeleme işleminde plastik deformasyon süresince meydana gelebileceği gibi haddeleme pasoları arasında ve haddeleme sonrasında metalin oda sıcaklığına soğuması sırasında da meydana gelebilir. Genel olarak haddelemede yeniden kristalleşme üç şekilde meydana gelebilir: Eğer yeniden kristalleşme deformasyondan sonra meydana geliyorsa buna statik yeniden kristalleşme (SYK) denir. Belirli şartlar gerçekleştiği taktirde yeniden kristalleşme deformasyon esnasında da meydana gelebilir. Buna dinamik yeniden kristalleşme (DYK) denir. Bazı durumlarda ise dinamik yeniden kristalleşme çekirdeklenme ile başlar fakat deformasyon süresince tamamlanamaz. Bu tür durumlarda deformasyon sonrası tamamlanan yeniden kristalleşmeye metadinamik yeniden kristalleşme denir ( MDYK).

Haddeleme işlemi sırasında dislokasyon yoğunluğu belirli bir seviyeye ulaştığı zaman dinamik yeniden kristalleşme (DYK) meydana gelir. Bu kritik genleme miktarı olarak tanımlanır. de başlayan dinamik toparlanmanın sağladığı yumuşama, olarak tanımlanan kritik bir değeri aştığında baskın hale gelir. Yani, den itibaren giderek azalarak da olsa görülen pekleşme, aşıldığında yerini yumuşamaya bırakır. Dinamik olarak oluşan taneler deformasyon sonrasında büyümeye devam ederek metadinamik yeniden kristalleşmye neden olurlar. Genleme değeri den az olduğu durumlarda haddelme sonrası statik yeniden kristalleşme meydana gelir. Bu alanda AISI 304 çeliği ile 1000 °C ve 0.5 s genleme hızında yapılan deneylerde kritik ve maksimum genleme miktarları sırasıyla için 0.5 ve için 0.7 olarak bulunmuştur. (H.W Lee , P.D Hodgson ,2006).

2.2.1 Statik Yeniden Kristalleşme

Statik yeniden kristalleşmenin kinetiği faz dönüşümlerininkine benzer. Statik yeniden kristalleşme prensip olarak iki aşamaya ayrılır. Çekirdek oluşumu ve büyüme safhaları. Yeni tanelerin oluşmaya başlaması çekirdeklenme safhası olarak adlandırılır. Oluşan yeni taneler haddeleme sırasında deformasyona uğramış tanelerin yerini alır. Statik yeniden kristalleşme sırasında tane büyümesine yol açan itici kuvvet ise deformasyon enerjisidir. Haddeleme sırasındaki statik yeniden kristalleşmeyi ifade eden en popüler denklem Johnson – Mehl- Avrami- Kolmogorov tarafından ortaya koyulandır (Lee Youngseog, 2004 ) Statik olarak yeniden kristalleşen bölgenin hacmi haddelemede deformasyondan sonra geçen zamanın cinsi şeklinden ifade edilmektedir:
X =1- exp (2.2)
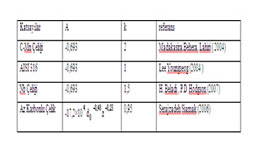
Bu denklemdeki k malzemeye bağlı sabit , t deformasyondan sonraki bekleme süresi , t ise malzemenin 50 sinin yeniden kristalleşmesi için geçen süredir. (2.2) eşitliğindeki sabitler Tablo 1 de verilmektedir:





Tablo 1 . Statik yeniden kristalleşmeye uğramış kısım denkleminin sabitleri
Katsayılar A k referans
C-Mn Çeliği -0,693 2 Madakasira,Behera, Lahiri ( 2004)
AISI 316 -0,693 1 Lee Youngseog (2004 )
Nb Çeliği -0,693 1,5 H. Beladi , P.D Hodgson (2007)
Az Karbonlu Çelik -17,2×10 d z
0,95 Serajzadeh Siamak (2006)


Haddeleme süresince meydana gelecek statik yeniden kristalleşme hacim oranını bulmak için öncelikle t değerini ifade etmek gerekir .
(2.3)
deformasyon miktarı , ise deformasyon hızıdr. ise deformasyondan önceki tane boyutudur. B, p , q , Q ise malzeme sabitleridir . (2.3) eşitliğindeki sabitler Tablo 2 de verilmektedir:


Tablo 2 . Malzemenin 50 statik yeniden kristalleşmeye uğraması için gereki süre denklemi için sabitler
Katsayılar B p Qrx referans
C-Mn Çeliği 2,5
-4 300000 Madakasira,Behera, Lahiri ( 2004)
AISI 316 1,14
-3,8 252000 Lee Youngseog (2004 )
Nb Çeliği 2,35×10
-3,5 250000 H. Beladi , P.D Hodgson (2007)
Az Karbonlu Çelik 4.43×10
-2,23 158000 Serajzadeh Siamak (2006)



Statik yeniden kristalleşmeden sonraki tane boyutu ise ;

(2.4)

Denklemde verilen C , C , m, n , l ve Q değerleri sabitlerdir. Haddeleme işlemi sırasında çoğunlukla pasolar arasında kismi yeniden kristalleşme görülür. Bu durumda kismi olarak yeniden kristalleşmiş tanenin ortalama tane boyutu ;

D= D + D (2.5)

Bu denklemde verilen D değeri haddede bir sonraki pasoya girmeden önceki ortalama tane boyutudur. Haddeleme işleminde ard arda gelen pasolar arasında meydana gelen toplam deformasyon miktarı ;

(2.6)

ile ifade edilir. ( i ) değeri toplam paso sayısını göstermektedir.

2.2.2 Dinamik Yeniden Kristalleşme
Dinamik yeniden kristalleşmenin mekanizması maksimum genleme miktarı ile kritik genleme miktarı ile ifade edilir. Denklem (2.7) de gösterildiği gibi maksimum genleme miktarı östenit tane boyutu ve sıcaklığa bağlı genleme hızına ( Zener Holloman parametresi ) bağlı olarak ifade edilirken , dinamik yeniden kristalleşmeye neden olan kritik genleme miktarı , ‘nin 60- 80 ‘ni arasında bir değer denk gelmektedir.

=A (2.7)
(A) sabit, (Z) Zener Holloman değişkeni;
Z= (2.8)
D ise tane boyutudur. Sıcaklık ve deformasyon hızı , Zener Hollomon parametresinde de belirttiği üzere tane boyutunu etkileyen başlıca parametrelerdir. (2.7) numaralı denklem için sabitler Tablo 3 de verilmektedir:


Tablo 3 . Dinamik yeniden kristalleşme için kritik genleme denklemi sabitleri
Katsayılar A p q referans
C-Mn Çeliği 4,9 × 10
0,17 0,3 Madakasira,Behera, Lahiri ( 2004)
AISI 316 6,97×10
0,17 0,3 Lee Youngseog (2004 )
Nb Çeliği 5,10×10
0,17 0,3 H. Beladi , P.D Hodgson (2007)
Az Karbonlu Çelik 6,5×10
0,132 0,43 Serajzadeh Siamak (2006)







Dinamik yeniden kristalleşmiş tane boyutu

D = BZ (2.9)
Dinamik yeniden kristalleşmenin kinetiği genellikle, deformasyon miktarını zamanın yerine bağımsız değişken kullanılarak elde edilir. Dinamik yeniden kristalleşmiş hacim oranı X ile ifade edilir.
X =1- exp (2.10)
(2.11)
Buradaki m Avrami sabiti olarak bilinir . Avrami denkleminden çıkarılan bu ifadeye göre dinamik olarak yeniden kristalleşen tane hacim oranı kritik deformasyon miktarına, yumuşama hızına bağlıdır (Y.Lee , P.D Hodgson, 2001). (2.10) numaralı denklem için sabitler Tablo 4 de verilmektedir

Tablo 4 . Dinamik yeniden kristalleşmeye uğramış kısım oranı denklemi sabitleri
Katsayılar B k referans
C-Mn Çeliği - 0.693 1 Madakasira,Behera, Lahiri ( 2004)
AISI 316 -0,8 1,4 Lee Youngseog (2004 )
Nb Çeliği -0,682 2 H. Beladi , P.D Hodgson (2007)
Az Karbonlu Çelik -17,2×10 d z
1,6 Serajzadeh Siamak (2006)



Dinamik yeniden kristalleşme sürekli olarak devam eden bir mekanizma olduğu için yeni tanelerin oluşumu ve dolayısı ile tane sınırları sürekli yer değiştirir. Bu nedenle deformasyon miktarı ile birlikte dinamik olarak yeniden kristalleşen tane hacim oranı artar. 100 dinamik yeniden kristalleşmiş malzemede tane boyutu sabit bir haldedir (Y.Lee , P.D Hodgson, 2001) :

(2.12)
Tablo 5 . Dinamik yeniden kristalleşme denklemleri
Form Not
n, A ; malzeme sabiti

k,n,; malzeme sabiti
dinamik yeniden kristalleşme sağlayan deformasyon

deformasyon miktarı

2.2.3 Metadinamik Yeniden Kristalleşme

Statik ve metadinamik yeniden kristalleşme yumuşama mekanizması açısından benzer olmasına karşın, statik yeniden kristalleşme büyük oranda deformasyondan sonraki bekleme süresine bağlı iken, metadinamik yeniden kristalleşme de durum böyle değildir. İki durum arasındaki diğer bir önemli fark ise; statik yeniden kristalleşme haddeleme esnasında herhangi bir yeniden kristalleşme meydana gelmeden oluşur. Oysa, metadinamik yeniden kristalleşme her zaman dinamik yeniden kristalleşme olduktan sonra meydana gelir. Statik yeniden kristalleşmenin aksine, metadinamik yeniden kristalleşmede çekirdeklenme süreci için herhangi bir süreye ihtiyac yoktur. Çünkü dinamik yeniden kristalleşmede oluşan tanelerden yararlanılır. Metadinamik yeniden kristalleşen tanelerin hacim oranını veren formül statik yeniden kristalleşmedekinin aynısıdır sadece sabitlerin değeleri farklıdır ( H. Beladi , P.D Hodgson , 2007)

X =1- exp (2.14)

(2.15)


Q deformasyon için aktivasyon enerjisidir. (2.14) numaralı denklem için sabitler Tablo 6 de verilmektedir:
Tablo 6 . Metadinamik yeniden kristalleşmeye uğramış kısım oranı deklemi sabitleri
Katsayılar A k referans
C-Mn Çeliği -0,693 1,5 Madakasira,Behera, Lahiri ( 2004)
AISI 316 -0,693 1,5 Lee Youngseog (2004 )
Nb Çeliği -0,693 1,2 H. Beladi , P.D Hodgson (2007)
Az Karbonlu Çelik -17,2×10 d z
1,2 Serajzadeh Siamak (2006)

(2.15) numaralı denklem için sabitler Tablo 7de verilmektedir:
Tablo 7 . 50 Metadinamik yeniden kristalleşmeye uğraması için gerekli süre deklemi sabitleri
Katsayılar A Qd referans
C-Mn Çeliği 1,06×10
300000 Madakasira,Behera, Lahiri ( 2004)
AISI 316 1,1 230000 Lee Youngseog (2004 )
Nb Çeliği 1,05×10
250000 H. Beladi , P.D Hodgson (2007)
Az Karbonlu Çelik 1,23×10
135000 Serajzadeh Siamak (2006)


Metadinamik yeniden kristalleşen tanelerin ortalama tane boyutu ;
D = A Z (2.16)
Haddeleme işleminde dinamik ve metadinamik olarak yeniden kristalleşmeye uğramış tanenin ortalama boyutu
D=D + (2.17)

X metadinamik olarak yeniden kristalleşen tanelerin hacim oranını vermektedir. (2.16) numaralı denklem için sabitler Tablo 8 de verilmektedir:




Tablo 8 . Metadinamik yeniden kristalleşmeye uğramış tane boyutu deklemi sabitleri
Katsayılar A u referans
C-Mn Çeliği 1,8
-0,15 Madakasira,Behera, Lahiri ( 2004)
AISI 316 2,6×10
-0,23 Lee Youngseog (2004 )
Nb Çeliği 1,5×10
-0,25 H. Beladi , P.D Hodgson (2007)
Az Karbonlu Çelik 520d
-0,08 Serajzadeh Siamak (2006)

2.3 Tane Büyümesi

Tane sınırlarında fazla enerji biriktiği zaman tane toplam tane sınır yüzeyini azaltarak büyüme yoluna gider. İlk tane boyutu ve haddeleme esnasındaki sıcaklık tane büyümesini önemli ölçüde etkiler. Küçük taneler büyüklerine oranla daha hızlı büyürken yüksek sıcaklıklarda büyüme daha hızlı gerçekleşir . Çözünen atomların ve katışkıların varlığı da tane büyümesini etkileyen diğer faktörlerdir. Haddeleme işlemi sırasında meydana gelen üniform büyümeyi ifade eden denklem (Y.Lee , P.D Hodgson, 2001).
(2.18)
büyüme geçirmiş tane boyutu , t yeniden kristalleşme tamamlandıktan sonra geçen süre , Q tane büyümesi için gerekli olan aktivasyon enerjisidir. N ve k malzeme sabitleri , D ise statik veya metadinamik olarak yeniden kristalleşmiş tane boyutudur.
(2.18) numaralı denklem için sabitler Tablo 9 da verilmektedir:
Tablo 9 . Statik yeniden kristalleşmede tane büyümesi katsayıların değişimi deklemi sabitleri
Katsayılar n k Qgg referans
C-Mn Çeliği, t - 4.3t > 1s
7 1.45
-400000 Madakasira,Behera, Lahiri ( 2004)
AISI 316, t - 4.3t < 1s
2 4×10
-113000 Lee Youngseog (2004 )
AISI 316, t - 4.3t > 1s
7 1.5
-400000 Lee Youngseog (2004 )

Eğer kısmi yeniden kristalleşme meydana gelmiş ise ortalama tane boyutu karışım kuralı ile bulunur (Y.Lee , P.D Hodgson, 2001).
t - 4.3t < 1s (2.19)
t - 4.3t > 1s (2.20)

(2.19) ve (2.20) numaralı denklemleri için sabitler Tablo 10 da verilmektedir:

Tablo 10 . Metadinamik yeniden kristalleşmede tane büyümesi katsayıların değişimi deklemi sabitleri
Katsayılar n k Qgg referans
C-Mn Çeliği, t - 4.3t > 1s
10 5.02
-914000 Madakasira,Behera, Lahiri ( 2004)
AISI 316, t - 2,65t < 1s
2 1,2×10
-113000 Lee Youngseog (2004 )
AISI 316, t - 2.65t > 1s
7 8,2
-400000 Lee Youngseog (2004 )



3. ÇELİKLERİN HADDELENMESİNDE MEKANİK ÖZELLİK MODELLERİ

Haddeleme prosesinde plastik olarak şekil değiştiren çeliklerin sıcaklık , genleme hızı , genleme miktarı ve kimyasal kompozisyonuna bağlı olarak plastik davranışlarını ortaya koyan çeşitli matematiksel modeller oluşturulmuştur. Bu denklemlerde genleme , sıcaklık , genleme hızı parametrelerinin gerilme değeri ile ilişkisi ortaya koyulmuştur. Oluşturulan denklemlerden bazıları aşağıdaki gibidir .

3.1 Zyunzin Denklemi
Aşağıdaki denklem değişik kalite çelikler üzerinde yapılmış olan deneyler sonucunda ortaya koyulmuştur. Zyunzin in denkleminin uygulama aralığı 900 ile 1200 oC ve 10 ile 10 s arasında işlem görüp genleme değeri 0,5 den az olan çelikler için uygulanmaktadır.
(3.1)
Denklemdeki sabitler aşağıdaki gibidir ;
= Herhangi bir kimyasal komposizyondaki malzeme için akma gerilmesi değeri
=Sıcaklık parametresi için katsayı
=Genleme değeri için katsayı
= Genleme hızı için katsayı
Sıcaklık ve genleme hızı aralığının dar olması nedeniyle sadece sınırlı sayıda çelik mamule uygulanabilir.

3.2. Misaka Denklemi

Aşağıdaki denklem ile deformasyona karşı malzemede meydana gelen ortalama direnci sıcaklık , genleme , genleme hızı ve karbon içeriğinin fonksiyonu olarak saptanmıştır.
(3.2)

Denlemde T sıcaklık ve [C] ise karbon içeriğini ifade etmektedir. Bu denklemin uygulama aralığı ise 1.2 karbona , 750-1200 oC arası sıcaklığa , 0.5 kadar genleme ile 30-200 genleme hızları arasındadır.

3.3 Shida Denklemi
Bu denklemin uygulama aralığı ise 0.07-1.2 karbon , 700-1200 oC arası sıcaklığa , 0.7 kadar genleme ile 100 genleme hızı arasındadır. Çeliklerin plastik şekil verme sırasında akma dayanımının ( ) karbon içeriği , genleme , genleme hızı ve malzemenin deformasyon direnç fonksiyonu ) ve normalizasyon sıcaklığı ( T ) nin fonksiyonu olarak ifade edilmektedir;
(3.3)

Deformasyon direnç fonksiyonu ise ;

T >T (3.4)
veya
T T (3.5)

T = ve T =0.95 (3.6)

Bu denklemlerdeki T Celcius cinsinden sıcaklığı ifade etmektedir. Yukarıda verilen denklemlerde T sıcaklığı T sıcaklığını aşarsa malzemede faz dönüşümü meydana gelmektedir. Denklem (3.5) de görüldüğü üzere, östenit fazının akma dayanımı içerdiği karbon miktarından daha çok sıcaklığa bağlı olarak değişmektedir. İşlem sıcaklığı değeri düştükçe çelikteki akma dayanımı üstel olarak artmaktadır. Akma dayanımı malzeme faz dönüşümü gösterirse değişmektedir ;

g(C,T )=30(C+0.9) (3.7)

Gerilme değeri normalizasyon sıcaklığı 0.95(C+0.49/C+0.42) değerine ulaşana dek düşer , fakat normalizasyon sıcaklığı 0.95(C+0.49/C+0.42) değerini aştığı zaman tekrar artmaya başlar. Bunun fiziksel açıklaması normalizasyon sıcaklığı ilk ferrit dönüşümüne ulaştığında , akma dayanımı sıcak düşüşü ile birlikte hızlı bir şekilde düşer. Faz dönüşümü tamamlandıktan sonra akma dayanımı değerlerinde tekrar yükselme gözlenir. Genleme ve genleme hızının etkisini gösterebilmek için Shida iki adet fonksiyon geliştirmiştir. Birisi, pekleşme fonksiyonu f ( ) :

f ( ) =1.3 n=0.41-0.07C (3.8)

Denklemden görüleceği üzere pekleşme değeri genleme 0.2 değerini aşmaya başlarsa düşmeye başlıyor. Denklemden de görüleceği üzere pekleşme değeri malzemenin içerdiği karbon miktarına göre düzenlenmiştir, sıcaklık değişimi ve genleme hızı etkili değildir. Diğeri, genleme hızı sertleşme fonksiyonu:

f ( )= (3.9)

Malzemenin genleme hızı sertleşmesi malzemenin genleme hızı 10 un üstüne çıkarsa yükselmeye başlar. Genleme hızı duyarlılık katsayısı m ;

m = (-0.019C+0.126) T + ( 0.076C-0.05) T >T
veya
m = (0.081C-0.154) T + ( -0.019C+0.207)+ T T (3.10)

yukarıdaki denklemler genleme hızı duyarlılığının büyük oranda sıcaklığa bağlı olduğunu açık bir şekilde göstermektedir. Genleme hızının gerilme üzerindeki etkisi malzeme faz dönüşümüne girdiği zaman hızla azalmaktadır. Shida ‘nın denklemi aynı zamanda mikro alaşımlar içeren çelikler için de kullanılabilir. Bu durumda çelik için şu eşdeğer karbon miktarı hesaplanmalıdır:
C = (3.11)

3.4 Johnson ve Cook Denklemi

Denklem malzemenin plastik deformasyonuna ve genleme hızına bağlı olarak dayanım değişimini ortaya koymuştur. Bu modele göre gerilmenin genleme , genleme hızı ve sıcaklığa bağlı olarak değişimi;

(3.12)

fonksiyonu ile ifade edilmektedir. Denklemdeki A, B , C , n ve k malzeme sabitleri olup regresyon analizleri sonucu ortaya çıkarılmışlardır. T , T ve T sırasıyla mevcut , referans ve erime sıcaklıklarıdır. Sabitler A, B , n ve C malzemenin kimyasal karışımının gücüne katkısını göstermektedirler.

H (t) (3.13)

H(t)= (3.14)
U(T) sıcaklığa bağlı bir adım fonksiyondur.

u ( T) = 0 T<T
1 T>T
T sıcaklığı dinamik yeniden kristalleşme veya faz dönüşümünün meydan geldiği sıcaklık değeridir. ve ise yeniden kristalleşme öncesi ve sonrası gerilme değerleridir.

4. SONUÇ

Yapılan bu çalışmada haddeleme sırasında oluşan mekanizmaları ve bunlara bağlı olarak malzeme bünyesinde meydana gelen mikroyapı değişimlerini ortaya koyan denklemler sunulmuştur. Verilen denklemler statik ,dinamik ,metadinamik yeniden kristalleşme , tane büyümesine ilişkin kinetikleri ortaya koymaktadır. Ayrıca haddeleme sıcaklığı , paso miktarı , haddeleme hızı ve karbon içeriğine bağlı olarak haddelenmiş çeliğin akma dayanımını veren en çok kullanılan ifadeler verilmiştir. Plastik deformasyon sırasında mikroyapının değişimi, sağlıklı olarak geliştirilecek malzeme modeli ile ortaya koyulabilir. Sıcaklığın zamanla değişimi sonlu elemanlar analzileri ile doğru olarak bulunabilir. Ortaya konulan bilgiler temel bilgileri ve değişkenleri içermektedir. Kuşkusuz bu alanda yapılacak birçok çalışmaya ihtiyaç duyulmaktadır

6. Kaynaklar

P.D Hodgson, W. Lee, 2006, Numerical investigation of austenite grain size distribution in hot bar
rolling , Journal of Materials Processing Technology, Volume 191, Issues 1-3, 1 August 007, Pages
114-118 Elsevier Ltd .

Lee Youngseog, 2004 , Rod and Bar Rolling , New York Publishing .
Y .Lee , P.D Hodgson , 2001, Integrated model for thermo mechanical controlled process in bar
rolling , Journal of Materials Processing Technology, Volumes 125-126, 9 September 2002, Pages
678-688 Elsevier Ltd .

Serajzadeh Siamak ,2006, A study on kinetics of static and metadynamic recrystallization during
hot rolling , Materials Science and Engineering: A, Volume 448, Issues 1-2, 15 March 2007, Pages
146-153 Elsevier Ltd .

H. Beladi , P.D Hodgson , 2007, Effect of carbon content on the recrystallization kinetics of NB
steels , Journal of Materials Processing Technology, Volumes 125-126, 9 September 2002, Pages 678-
688, Elsevier Ltd .

H. W Lee , P.D Hodgson , 2006 , Numerical investigation of austenite grain size distribution in square
diamond pass hot bar rolling , Journal of Materials Processing Technology, Volume 191, Issues 1-
3, 1 August 2007, Pages 114-118 ,Elsevier Ltd .

Madakasira Prabhakar Phaniraj ., Binod Bihari Behera, Ashok Kumar Lahiri , 2004 , Thermomechanical
modeling of two phase rolling and microstructure evolution in the hot strip mill ,Elsevier Ltd.



Tadamasa Shida ,1969, The Journal of Physical Chemistry J. Phys. Chem. 0022-3654 American
Chemical Society

Misaka & T. Yoshimoto,1967, J. Japan Soc. Technol. Plast., vol. 8, p. 414. 2. S.
G.R. Johnson, W.H. Cook,1983 , Johnson-Cook model International Symposium on Ballistics.
Netherlands.


7 . Özgeçmiş

Barış AKYALÇIN , 1983 yılında İstanbulda doğdu . İlköğretimini İstanbulda Deniz İş İlköğretim okulunda tamamladı. 2001 yılında Kabataş Erkek Lisesinden Mezun oldu. Aynı sene Yıldız Teknik Üniversitesi Makine Mühendisliği Bölümüne girip 2005 yılında Genel Makine Bölümünden mezun oldu. Aynı sene güz döneminde İTÜ Malzeme ve İmalat Ana bilim Dalında Yüksek Lisans Eğitimine Başladı. Halen yüksek lisans eğitimi devam etmekte olup, çalışmayı birlikte hazırladığı Doç.Dr Şafak Yılmaz ile Çeliklerin Haddelenmesinde Malzeme Modelleme konusunda tez çalışması yapmaktadır

. . .

İçerik sadece atıfta bulunularak yayınlanabilir: Sivas İş Dünyası. Editöryal görüş, yazarın görüşüne aykırı olabilir.